CSC447

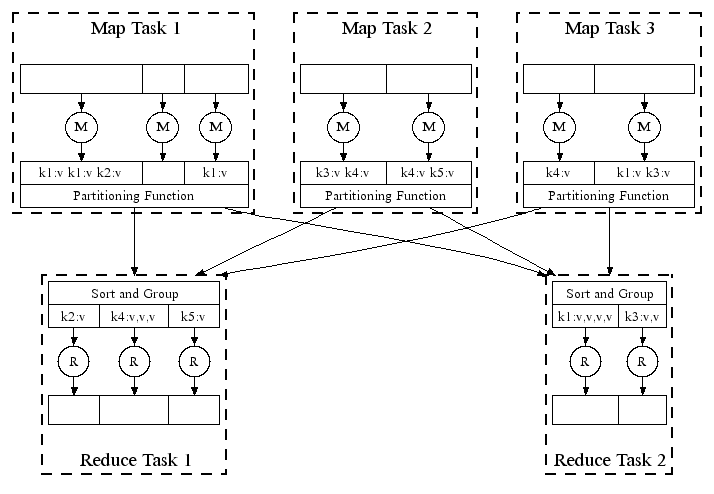
Map-Reduce Frameworks

def map(name: String, contents: String) = 
  for w <- contents do
    emit (w, 1)
 
def reduce(word: String, partialCounts: Iterator) = 
  var sum = 0
  for pc <- partialCounts do
    sum = sum + pc
  emit (word, sum)

Parallel Execution

Sum computing forward

def sum (xs:List[Int], z:Int = 0) : Int =  xs match 
  case Nil   => z
  case x::xt => sum (xt, z + x)
 
val xs = List(11,21,31)
sum (xs)

sum(11::21::31::Nil)
--> sum(11::21::31::Nil, 0)
--> sum(21::31::Nil, 11)
--> sum(31::Nil, 32)
--> sum(Nil, 63)
-->
-->
-->
--> 63 = (((0 + 11) + 21) + 31)

Sum computing backward

def sum (xs:List[Int], z:Int = 0) : Int =  xs match 
  case Nil   => z
  case x::xt => x + sum (xt, z)
 
val xs = List(11,21,31)
sum (xs)

sum(11::21::31::Nil)
--> sum(11::21::31::Nil, 0)
--> 11 + sum(21::31::Nil, 0)
--> 11 + (21 + sum(31::Nil, 0))
--> 11 + (21 + (31 + sum(Nil, 0)))
--> 11 + (21 + (31 + 0))
--> 11 + (21 + 31)
--> 11 + 52
--> 63 = (11 + (21 + (31 + 0)))

Sum to foldLeft

def sum       (xs:List[Int], z:Int)                     : Int =  
  xs match 
    case Nil   => z
    case x::xt => sum       (xt, z + x)
 
val xs = List(11,21,31)
sum       (xs, 0)

res1: Int = 63

Sum to foldLeft

def foldLeft  (xs:List[Int], z:Int, f:((Int,Int)=>Int)) : Int = 
  xs match 
    case Nil   => z
    case x::xt => foldLeft  (xt, f(z,x), f)
 
val xs = List(11,21,31)
foldLeft  (xs, 0, (z:Int, x:Int) => z + x)

res1: Int = 63

Function Parameters

def foldLeft  (xs:List[Int], z:Int, f:((Int,Int)=>Int)) : Int = ...

• takes an argument of type (Int,Int)
• returns a result of type Int

Changing the return type

def foldLeft  (xs:List[Int], z:String, f:(String,Int)=>String) : String = 
  xs match 
    case Nil   => z
    case x::xt => foldLeft  (xt, f(z, x), f)
 
val xs = List(11,21,31)
foldLeft  (xs, "!", (z:String, x:Int) => z + "0x%02x".format(x))

res1: String = !0x0b0x150x1f

Changing the parameter type

def foldLeft  (xs:List[List[Int]], z:Int, f:(Int,List[Int])=>Int) : Int = 
  xs match 
    case Nil   => z
    case x::xt => foldLeft  (xt, f(z, x), f)
 
val xss = List(List(11,21,31),List(),List(41,51))
foldLeft  (xss, 0, (z:Int, x:List[Int]) => z + x.length)

res1: Int = 5

Type parameters

def foldLeft  [Z,X] (xs:List[X], z:Z, f:((Z,X)=>Z)) : Z =
  xs match 
    case Nil   => z
    case x::xt => foldLeft  (xt, f(z,x), f)
 
val xs = List(11,21,31)
foldLeft  (xs, "!", (z:String, x:Int) => z + "0x%02x".format(x))

res1: String = !0x0b0x150x1f

Fold Right

def foldRight [X,Z] (xs:List[X], z:Z, f:((X,Z)=>Z)) : Z =
  xs match 
    case Nil   => z
    case x::xt => f (x, foldRight (xt, z, f))
 
val xs = List(11,21,31)
foldRight (xs, "!", (x:Int,z:String) => "0x%02x".format(x) + z)

res1: String = 0x0b0x150x1f!

Left v Right

def foldLeft  [Z,X] (xs:List[X], z:Z, f:((Z,X)=>Z)) : Z =
  xs match 
    case Nil   => z
    case x::xt =>
      val r = f(z, x)
      foldLeft  (xt, r, f)

def foldRight  [Z,X] (xs:List[X], z:Z, f:((Z,X)=>Z)) : Z =
  xs match 
    case Nil   => z
    case x::xt =>
      val r = foldRight  (xt, z, f)
      f(x, r)

Left v Right

• foldLeft computes f into a parameter:
  • return foldLeft (xt, f(z, x))
    • apply f to the head and the accumulated result
    • recursive call on the tail
  • base case used with first element
• foldRight is computes f into the result:
  • return f (x, foldRight (xt, z))
    • recursive call on the tail
    • apply f to the head and result of recursion
  • base case used with last element

Builtin folds

• Scala List class has fold methods

  xss.foldLeft (0) ((z,xs)=>z + xs.length)

  vs our own foldLeft function

  foldLeft (xss, 0, (z,xs)=>z + xs.length)

• Operator forms:

   xss.foldLeft(0)(f) == (0 /: xss)(f)
  xss.foldRight(0)(f) == (xss :\ 0)(f)

Left v Right

def foldLeft [Z,X] (xs:List[X], z:Z, f:((Z,X)=>Z)) : Z =  xs match 
  case Nil   => z
  case x::xt => foldLeft (xt, f(z,x), f)

def foldRight [X,Z] (xs:List[X], z:Z, f:((X,Z)=>Z)) : Z =  xs match 
  case Nil   => z
  case x::xt => f (x, foldRight (xt, z, f))

val xs = List(a, b, c)
foldLeft (xs, z, f) === f( f( f(z,a),b),c) === (z /: xs)(f)
foldRight(xs, z, f) === f(a, f(b, f(c,z))) === (xs :\ z)(f) 

                   (z /: xs)(f)           (xs :\ z)(f)
                      f                       f
                     / \                     / \
                    f   c                   a   f
                   / \                         / \
                  f   b                       b   f
                 / \                             / \
                z   a                           c   z

Folds are universal

def sum         (xs: List[Int])              = xs.foldLeft(0)(_+_)
def prod        (xs: List[Int])              = xs.foldLeft(1)(_*_)
def or          (xs: List[Boolean])          = xs.foldLeft(false)(_||_)
def and         (xs: List[Boolean])          = xs.foldLeft(true)(_&&_)
def append  [X] (xs: List[X])(ys: List[X])   = xs.foldRight(ys)(_::_)
def flatten [X] (xs: List[List[X]])          = xs.foldLeft(Nil:List[X])(_:::_)
def length  [X] (xs: List[X])                = xs.foldLeft(0)((z,x)=>z+1)
def reverse [X] (xs: List[X])                = xs.foldRight(Nil:List[X])((x,zs)=>zs:::List(x))
def map   [X,Y] (xs: List[X], f: X=>Y)       = xs.foldRight(Nil:List[Y])(f(_)::_)
def filter  [X] (xs: List[X], f: X=>Boolean) = xs.foldRight(Nil:List[X])((x,zs)=>if f(x) then x::zs else zs)

Here are lots and lots of foldleft examples

A tutorial on the universality and expressiveness of fold